One for trigonometry gurus here

dal

dal

dal

Associate
Joined
10 Sep 2005
Posts
909
Location
Lincolnshire
Hello, looking at the image below, is it possible to find the distance of line A-B and line B-C

Obviously the angle I've not shown is 110 degrees( 180 - 57-13 )


Thanks.
( Please show how you got to the figures )

 
dal said:
Hello, looking at the image below, is it possible to find the distance of line A-B and line B-C

Obviously the angle I've not shown is 110 degrees( 180 - 57-13 )


Thanks.
( Please show how you got to the figures )

Click to expand...

Of course it is :D

(Just haven't had to do this for 30 years so I will have to think about it)

What is the back ground picture

(That is much more interesting!)
 
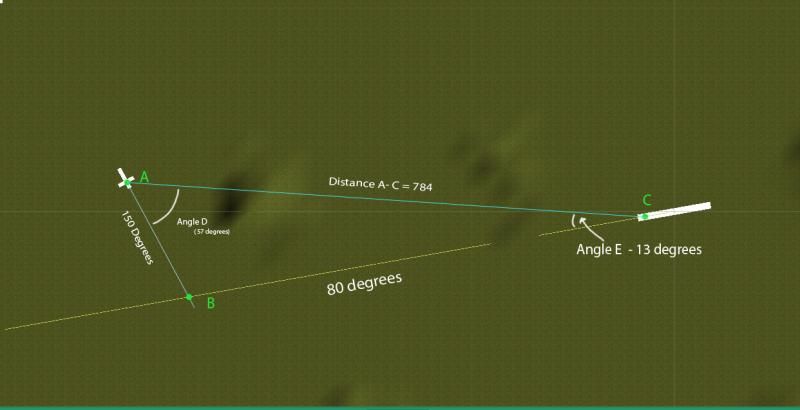
Background picture is a screen shotr from a air traffic control game I'm making. The yellow line is in line with the runway centre line.

@ bitslice - how did u get those figures
 
dal said:
Background picture is a screen shotr from a air traffic control game I'm making. The yellow line is in line with the runway centre line.

@ bitslice - how did u get those figures
Click to expand...

It'll be the sine rule. Really easy to use. Just 3 ratios that must be equal.
 
dal said:
Background picture is a screen shotr from a air traffic control game I'm making. The yellow line is in line with the runway centre line.

@ bitslice - how did u get those figures
Click to expand...

Aw Shute!

And there was I thinking this was some sort of google earth finding Genghis Khans tomb thing!

:(
 
bitslice said:
Odd, just tried the sine rule and got different figures from my first go.

What we need are some Economic students to give us a clue
Click to expand...

Well I'm economics graduate.

I'd only give you different answers if the angles keep changing :p
 
If it's not 110, that just implies you've measured the other angles badly. :p

edit: teacher I misread the question
 
Last edited:
Not sure how Bitslice got 878 for B-C when it's obviously shorter than A-C

A-B - 209.2
B-C - 780.0

To 1 decimal place.

For my ease as it's the way I sketched it out and labelled it. Sorry.... May not help that much. It's essentially flipped horizontally. Wasn't paying that much attention.

It's the Law of Sines, and because you know the angles and one of the side you can jump straight into the equations needed.

Code: 
     bsinA
a= ---------
     sinB


     csinA
a= ---------
     sinC


     asinB
b= ---------
     sinA


     csinB
b= ---------
     sinC


     asinC
c= ---------
     sinA


     bsinC
c= ---------
     sinB



Angles
13° = A
110° = B
57° = C

Sides
AB = a
AC = b = 874
BC = c

You know A B and C and b

So, to get side c
Code: 
    bsinC
c= -------
     sinB

   874sin(57°)
c= -----------
    sin(110°)

c= 780.04026


To get side a

Code: 
     bsinA
a= ---------
     sinB


   874sin(13°)
a= ----------
    sin(110°)

a= 209.225035

And now... I'm off to bed as this has brought back painful A-Level memories.
 
My little excel trig file doesn't agree with anyone!

A-B 176.3616
B-C 763.90613

XRxGJ7i.jpg.png
 
Last edited:
You need a right-angled triangle for sin, cos, and tan to work. Drop a line from point B that hits line AC at a right angle. You then have two right-angled triangles whose angles you know. Then set up some simultaneous equations for one of the triangles and solve them for the length of the common side (the one we made). Calc the rest from trig identities.
 
You must log in or register to reply here.
Back
Top Bottom