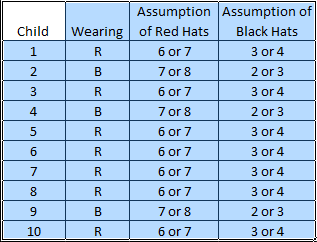
Maybe the person who wrote the riddle worked out that you need that information for 0, 1 and 2 red hats (although I'm still not clear on 2 if I'm honest as it still isn't 'new information'), stopped there and presumed that would continue to be true no matter how much you scale up?
Assume we know theres two colours and at least one of each.
For 2 hats
=======
If theres 2 red hats, when #1 looks around and sees another red hat, he doesn't know if theres 1 or 2 hats so he can't say.
#2 red knows #1 red saw another red, can't see any more reds, so assumes it's himself.
For 3
=======
#1 red sees 2 red, but doesn't know if theres 2 or 3.
#2 red sees 2 red, knows theres at least 2 and accepts that #3 might be what #1 say to say "I don't know".
#3 sees 2. Knows that #1 sees 2 (not including #1) and #2 sees 2 (not including #2) so by looking about he can figure out its himself.
For 4
====
#1 red sees 3 red, but doesn't know if theres 3 or 4.
#2 red sees 3 red, knows theres 3 or 4 but can only know #1 sees at least up to 2.
#3 red sees 3, he knows theres either 3 or 4, but knows #1 can see 2 and #2 can see 2 but not whether either of them can see 3.
#4 can see 3. He knows that if there was 3 hats, #3 should have been able to guess the colour so he's able to deduct theres 4 hats and since he can only see 3, it's him.
You can continue this for infinity, as it'll always come down to "the number before me should have guessed this if it if there was n-1 hats.
The class needs to know theres only two colours at least 1 of each. The reason they need to knows theres at least one red is because when you have only 1 in play, the guy can assume theres 0, where as when theres 2 in play, red #2 can't assume red #1 actually sees any reds because there might be 0.
When you have 3 reds in play. #1 can see 2. #2 can see 2. #3 knows they can both see 1 and normally would assume #2 should have guessed but since #2 might only see 1 red and #2 might think #1 can see 0, #3 can't actually solve it.
So yeah the riddle worked, I'm just slow until I wrote it down.



 .
.