Mid-Week Brain Teaser

[estebanrey]

But the kid with the red hat wouldn't even know that there are red hats to begin with in that situation, so whilst he'd be right, he wouldn't KNOW he was right, which is the point . I meant that it'd work as in classroom 1 can't work it out and classroom 2 could, not that neither could, if you were referring to the second being able to work it out.

Yep, I see my bad. Accept my retraction

 

[AJK]

If no person in the first classroom could deduce the rule then no person in the second class could either as there has been no new 'information' introduced to them.

Yes there is!

Child 1 = 6 Red Hats Left, 8 Black
Child 2 = 6 Red Hats Left, 7 Black
Child 3 = 5 Red Hats Left, 7 Black
Child 4 = 4 Red Hats Left, 7 Black
Child 5 = 4 Red Hats Left, 6 Black
Child 6 = 4 Red Hats Left, 5 Black
Child 7 = 4 Red Hats Left, 4 Black
Child 8 = 3 Red Hats Left, 4 Black
Child 9 = 2 Red Hats Left, 4 Black
Child 10 = 1 Red Hat Left, 4 Black
Child 11 = 1 Red Hat Left, 3 Black
Child 12 = 1 Red Hat Left, 2 Black
Child 13 = 0 Red Hats Left, 2 Black
Child 14 = N/A
Child 15 = N/A

So child 13 knows that there are no more children left to ask with a red hat on but there are still 2 kids left wearing black hats. Because child 13 knows that child 10 said "I don't know" and that was the last person wearing a red hat who didn't have enough information to answer with certainty then they must be wearing a red hat.

Explain to me why, in your scenario, child 10 saying "I don't know" means that child 13 can be sure his hat is red?

 

[wesimmo]

You're correct here and I actually think that game 1 is solvable too. The difficulty is that in game 2 the teachers bit of information is actually more subtle than it may first appear.

By saying that there is at least 1 red, then it provides a situation not just where all players know there is a red, but also where they know that all other players know there is a red. A subtle but important difference.

In order to achieve this knowledge in game 1, I think there needs to be at least 3 'reds' (and at least 3 'blacks) in the starting condition. Which I believe there is in the OP's example and so it should be solvable using the same logic as game 2.

I disagree, in both scenarios all the kids know that there is at least 6 reds, because the minimum number a kid can see is 6.

And because they can see at least 6 reds, then they know every other kid can see at least 5 reds even if they assume they themselves are wearing a black hat.

Therefore every kid can deduce that all other kids know there are multiple red hats.

 

[estebanrey]

Yes there is!

What is new about it? You've ignored the coin example I gave you, given you can see there are four 1 pound coins in that picture what new information do I give you by saying "at least one coin there is a £1" after showing it to you?

All I've done is told you something you knew already from looking at the picture, hence it's not 'new' information.

Explain to me why, in your scenario, child 10 saying "I don't know" means that child 13 can be sure his hat is red?

Explain to me why Child 13 being told there is "at least one red hat" at the start of the game when at that point they know that already because they can see 6 other kids wearing one changes whatever you think the inductive logic is here first.

 

[div0]

I disagree, in both scenarios all the kids know that there is at least 6 reds, because the minimum number a kid can see is 6.

And because they can see at least 6 reds, then they know every other kid can see at least 5 reds even if they assume they themselves are wearing a black hat.

Therefore every kid can deduce that all other kids know there are multiple red hats.

Correct, that's what I'm saying. In the specific example given for game 1, there is sufficient information to end up effectively playing the game with the same knowledge as game 2.

Both are solvable.

All I was doing is pointing out that the teachers information in game 2 is actually more specific than you might first think. Meaning that game 1 is only solvable in certain starting situations.

 

[RDM]

Yes. There. Is.


Explain to me why, in your scenario, child 10 saying "I don't know" means that child 13 can be sure his hat is red?

Because he can see that all the red hat children have said "I don't know" and a black hat has said "I don't know." As he can see all other people that haven't answered have black hats then he knows that his hat has to be red. This is exactly the same for both scenarios.

The only difference between both scenarios is that group two has been specifically told something they already know.

 

[div0]

Yes there is!


Explain to me why, in your scenario, child 10 saying "I don't know" means that child 13 can be sure his hat is red?

Why does child 10 have to say 'I don't know'?

Child 10 can solve the puzzle, the same as in game 2 - for the reasons Estabaney states. All players start the game with sufficient knowledge to know that every player knows that there is at least 1 red, they don't need to be specifically told.

The subtly here is not simply for you as an individual to know that there is at least 1 red. You need a situation where (at the start of the game) all players know that all other players know, there is at least one red.

Starting with 7 reds is way more than enough to achieve this knowledge, without being specifically told by the teacher.

Likewise Game 2 is only solvable because we're told that 'a few blacks' have already been eliminated. This is basically the same as the teacher saying 'there was at least 1 black'. If there had been any less than a 'few blacks', then game 2 hits problems too.

 

[AJK]

What is new about it? You've ignored the coin example I gave you, given you can see there are four 1 pound coins in that picture what new information do I give you by saying "at least one coin there is a £1" after showing it to you?

All I've done is told you something you knew already from looking at the picture, hence it's not 'new' information.

I've said I don't know how many times, the "at least one red hat" statement is nothing whatsoever to do with how many hats you can or can't see. It is a logical statement necessary for the following statement to be true: If person 1 sees all black hats, he will know he is wearing a red one.

Explain to me why Child 13 being told there is "at least one red hat" at the start of the game when at that point they know that already because they can see 6 other kids wearing one changes whatever you think the inductive logic is here first.

No. The onus is on you to explain why you think your solution holds. I've explained here why it doesn't:
http://forums.overclockers.co.uk/showpost.php?p=23711588&postcount=59

 

[aln]

It isn't badly worded. There is exactly one new piece of information introduced in the second trial, which is the statement "there is at least one red hat". Observationally, this doesn't tell you anything (every child can see at least 6 red hats), but logically it does.

Spoiler

Consider the first classroom, who do NOT have the statement "there is at least one red hat":

Person 1 will ALWAYS say "I don't know", regardless of whether they see red hats, black hats, or a mixture of colours. They do not have enough information to deduce what colour their hat is.

Since person 1 will always answer "I don't know", person 2 can't draw any information from that answer, and thus can only base their own guess on the hats they can see - which, as for person 1, is not enough information to draw a conclusion and so person 2 will also always answer "I don't know".

This continues for persons 3, 4, 5, etc. It's impossible to reach a point where you can logically conclude "I see only black hats remaining, and nobody else knew the colour of theirs, so my hat must be red". It's not logically true.

This only works if the people who've had their answer remove their hats and discount the one red hat being on the people who have already went.

From the info we are given, there are 7 red hats and you were told there is at least one. You look around you see 6, thats more than one and since you do not know the total number, you cannot deduce what you have from this information alone.

I totally get the point of the deduction and when theres two hats in play and I'm told theres at least 1, then the second red hat should know he's red and the rest should know they're black based on his answer.

But I still think the riddle itself was ****** up and I hazard a guess the people agreeing with it are those that have read about this elsewhere and aren't taken the OP on what he's specifically said.

I could be being thick though, so please tell me how the last 1/2 red hat kids knows theres still 1 red hat in play unless they teacher told them it was so before they took their shot and they were specifically told to discount everyone who already answered.

 

[wesimmo]

Honestly i feel so dumb, i just can't see how this works...

The above table is my view of what each person can safely assume given that everyone knows...

-There are 10 people in the room.
-They are wearing either a red or black hat.

If they're wearing a red hat but are unaware of that fact, they can therefore deduce...

-There are 6 or 7 red hats in the room, and therefore 3 or 4 black hats

If they're wearing a black hat but are unaware of that fact, they can therefore deduce...

-There are 7 or 8 red hats in the room, and therefore 2 or 3 black hats

Everyone can therefore deduce that

-Everyone knows there are multiple red and black hats in the room.
-No one can guess what they are wearing.

What i don't then see is how someone saying "I don't know" changes any of the above?

 

[div0]

It isn't about people removing their hats, or hats 'leaving' the game.

It's about using what other players see (their knowledge, or lack of knowledge) to establish your hat, based on what others prior to you must have be looking at.

 

[RDM]

I've said I don't know how many times, the "at least one red hat" statement is nothing whatsoever to do with how many hats you can or can't see. It is a logical statement necessary for the following statement to be true: If person 1 sees all black hats, he will know he is wearing a red one.


No. The onus is on you to explain why you think your solution holds. I've explained here why it doesn't:
http://forums.overclockers.co.uk/showpost.php?p=23711588&postcount=59

In both scenarios mentioned by the OP the outcome is the same because the additional information supplied in scenario 2 is already known in scenario 1.

 

[aln]

It isn't about people removing their hats, or hats 'leaving' the game.

It's about using what other players see (their knowledge, or lack of knowledge) to establish your hat, based on what others prior to you must have be looking at.

Every player can see 6-7 red hats, that same as you can see. Knowing what they know doesn't help you unless you change the rules to the game.

Now if you had 2 red hats only in play, you can happily deduct you have a red hat based on your ability to see only 1 and that 1 guy saying "I don't know", but as soon as you add the 3rd red hat you cancel your ability to deduce that out.

 

[estebanrey]

I've said I don't know how many times, the "at least one red hat" statement is nothing whatsoever to do with how many hats you can or can't see. It is a logical statement necessary for the following statement to be true: If person 1 sees all black hats, he will know he is wearing a red one.

The logical statement you've said there is basically the same as the 'rule' I posted earlier in a shortened form.

That doesn't detract from the physical fact that the kids already know there is at least one from their physical observations at the start of the game thus making the teacher telling them it redundant and unnecessary.

Given we agree that every child in the game needs to know there is at least one red hat in the game, please explain why each and every child in the first group doesn't know this already and thus fails the task (or why the second group who are told this but already know it have an advantage).

No. The onus is on you to explain why you think your solution holds. I've explained here why it doesn't:
http://forums.overclockers.co.uk/showpost.php?p=23711588&postcount=59

Given pretty much everyone above disagrees with you and thinks that the first group can solve the problem without being told something they can already see, I'd say the onus was on you to clarify, or rather King Damager who seems to have shyed away from this issue by trying to introduce a new riddle

 

[AJK]

Because he can see that all the red hat children have said "I don't know" and a black hat has said "I don't know." As he can see all other people that haven't answered have black hats then he knows that his hat has to be red. This is exactly the same for both scenarios.

This isn't conclusive. "As he can see all other people that haven't answered have black hats then he knows that his hat has to be red" - why? Why isn't it black? There has to be reasoning behind that statement.

 

[div0]

What i don't then see is how someone saying "I don't know" changes any of the above?

Think about what the 'other' players must be seeing.

First let's assume that all players know there is a mix of hats (at least one of each). This could be established by the teacher telling them, but can also be deduced visibly at the start of the game, but is a little complex to be done visibly, for the reasons I've already posted).

Anyway, let's assume that 1 bit of knowledge, as it is crucial (at least 1 of each hat).

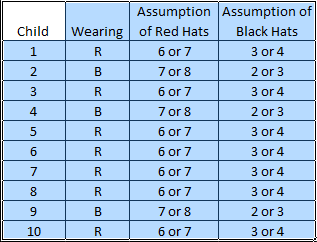
Player 1 sees a mix of hats, he has no idea what his hat is, so he says 'don't know'.

Player 2 knows what player 1's hat is, but also sees a mix of colours (2 blacks), so he says 'don't know'.

All other players know player 2 is black, so they know he saw at least 1 other black hat. If he didn't see other black hats, then he's the 1 and only back hat'.

We continue thus until player 4's turn. He also see's two black hat's (2 and 9). Now player 2 might have only seen 1 black (player 9), or he might have seen 2 (4,9). So he's unsure if he (4) is red or black and say's 'don't know'.

When we get to player 9's turn, he knows that if he's red, then player 4 must have only seen 1 black (2). And so player 4 would have won the game, knowing he (4) was the only black.

This means the player 4 must have seen 2 and 9 as black, which means that 9 knows he must be black.

Probably not explained the best, sorry.

 

[AJK]

... please explain why each and every child in the first group doesn't know this already and thus fails the task (or why the second group who are told this but already know it have an advantage).

What exactly is wrong with my logic here, except that you disagree with it?

Consider the first classroom:

Person 1 will ALWAYS say "I don't know", regardless of whether they see red hats, black hats, or a mixture of colours. They do not have enough information to deduce what colour their hat is.

Since person 1 will always answer "I don't know", person 2 can't draw any information from that answer, and thus can only base their own guess on the hats they can see - which, as for person 1, is not enough information to draw a conclusion and so person 2 will also always answer "I don't know".

This continues for persons 3, 4, 5, etc. It's impossible to reach a point where you can logically conclude "I see only black hats remaining, and nobody else knew the colour of theirs, so my hat must be red". It's not logically true.

 

[Bloomfield]

This isn't conclusive. "As he can see all other people that haven't answered have black hats then he knows that his hat has to be red" - why? Why isn't it black?

Because the person who said "I don't know" before him knew that red hats existed (as there was too many at the start for everyone to not know this). If he knew that red hats existed, and he didn't know whether he had a red hat it means that he can see someone with a red hat. If the person now guessing can't see a red hat then he knows that the red hat that other previous person saw was his.

 

[estebanrey]

This isn't conclusive. "As he can see all other people that haven't answered have black hats then he knows that his hat has to be red" - why? Why isn't it black?

Because the inference is if you don't have enough information to answer you say "I don't know". You do not have enough information whilst there are still people left who haven't been asked who are wearing a specific hat colour.

Hence, Child 13 (going back to my example) knows that child 10 was the last person to see people wearing hats of both colours yet to be asked. As child 13 can only see black hats left and everyone before him/her has said "I don't know" they know the child that Child 10 saw wearing a red hat was them.


You keep questioning the inductive thinking of the main problem in the riddle but this thinking is ulitamtely the same in both scenarios. If you can't work out why Child 13 would know their hat was not black then you aren't helped by introducing the statement "at least 1 hat is red" at the start of the game to Child 13 because, as has been explained many times, he or she already knows this anyway.

 

[RDM]

This isn't conclusive. "As he can see all other people that haven't answered have black hats then he knows that his hat has to be red" - why? Why isn't it black? There has to be reasoning behind that statement.

Everyone can see all hats bar their own. If you are in a red hat then once you see that all red hats you can see have said I don't know and that the next black hat has said I don't know(which means there is at least one other red hat) then the only remaining red hat has to be yours because you can see that all the remaining other hats are black. This is the same for both scenarios as described in the OP. The additional information supplied in scenario 2 is redundant because everyone can already see that there is at least one red hat.