Wimnat said:
OK so in the 32 bit buffer you have your sign bit and then the max number...
0 1111 1111 1111 1111 1111 1111 1111 111
and if you exceed this max number by one then rather than the number keeping the sign bit and overflowing the other side, the sign bit is overwritten?
2147483648 =
1 0000 0000 0000 0000 0000 0000 0000 000
and then if the number grows any bigger than 32 bits then memory overflows and the program exits?
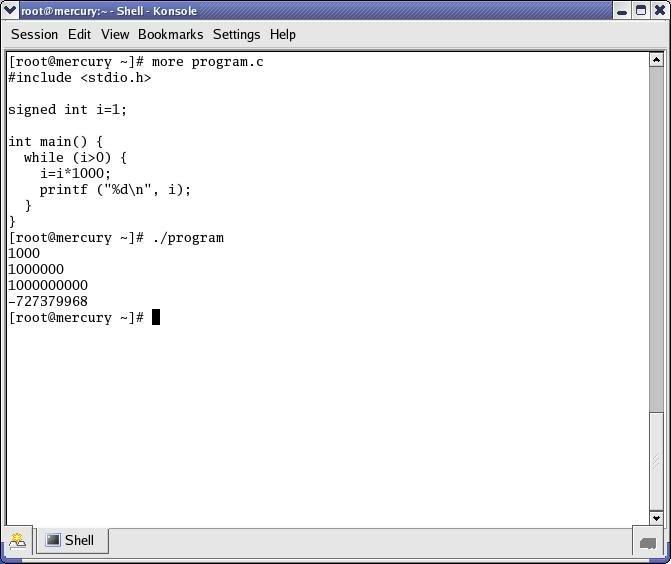
No. Nothing happened to the memory, and the program did not crash - it terminated normally.
The number the computer was trying to calculate was 1000000000000 (or 10^12). As others have said, this does not fit into a 32 bit integer. What you get is the lowest 32 bits of the result. As an analogy, suppose (in decimal) I have registers that only hold 2 digits. If I try to multiply 21x21, you'd expect to get 441, but the result will end up as only the bottom two digits; that is, 41.
In this case, 10^12 = 232*2^32 + 3567587328. That is, the lowest 32 bits of the result is 3567587328 (11010100101001010001000000000000 in binary). The reason the computer shows this as a negative number is because you are using a signed int, which means the top most bit represents -2^31 rather than 2^31. So the signed equivalent of 3567587328 is 3567587328 - 2^32, which is -727379968.
Nothing "bad" has happened during any of this (other than getting an answer you might not expect). Nothing happened to any stack, heap, etc. How coul it - your program makes no use of such resources. The reason the program terminates is simply because the answer is less than 0, and the condition in the while loop is "(i > 0)".
If you define i to be an "unsigned int", you will find the value of i on the 4th time around the loop is 3567587328 (as above), which is clearly wrong, but won't cause the program to terminate. Without checking, I think you'll find the program will now terminate after 11 iterations when the value of i will be zero. This is because 8 | 1000, so you are effectively adding 3 binary zeros on the end of i each time through. So after 11 iterations, the lowest 32 bits of i will be zero.