Engineering Dynamics Question - SHM

danza

danza

danza

Soldato
Joined
28 Mar 2005
Posts
13,679
Location
Drunken badger punching
I'm stuck. I have a question on simple harmonic motion and a solution to it, and I'm still stuck.

Basically, I can't get my head around how the solution is arrived at. It's just not going in/making sense.

Some fun pictures:

Relevant tutorial section (even with this I can't get my head around things)

DSC_0168_zpsezdra4rp.jpg


Question

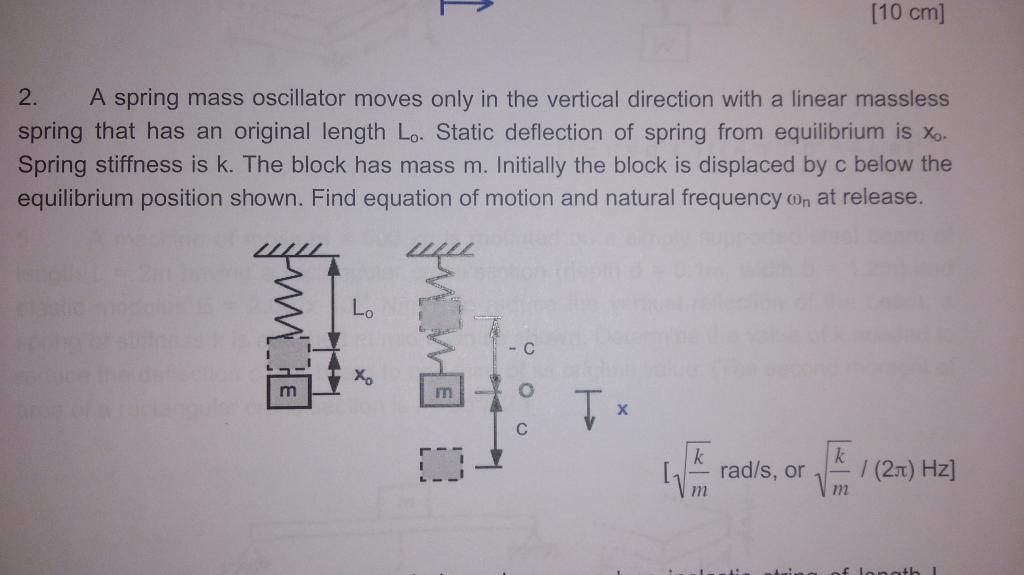
DSC_0166_zpsot1f1s9l.jpg


Solution

DSC_0167_zpsqkxadqji.jpg


Can anyone explain/help me remember how this is done in steps? It seems like some of the working is missing from the solution, or that there is a gap in my knowledge that's not letting me fill in the blanks.

I knew I shouldn't have waited 2 years before topping-up to a degree. :/

Any assistance would be spiffing.
 
From a quick look, I think the diagram may be labelled in the question wrong? I think Xo should be X and Lo should be Xo.

Then the generic EOM is F=MX + kX

Where F=MA

So MX = MA - k(Xo + X)

Then MA=-kx

so MX = kX - k(Xo+X) = KXo

Thefore MX-KXo = 0

Then I'm not sure how you get the natural frequency without more numbers as he's just written the forumulas given but it's late, it's been a while and I don't have my notes.

Hopefully some cleverer folk will be in soon :)
 
Anything specific you're struggling with?

First part is resolving forces,

Oscillation takes (omega)-n squared is the preceeding value to x(dot), in this case k/m (and thus omega is sqrt)

(do you know that X double dot is acceleration?)
 
Last edited:
I have no idea what the author has done here. It looks like he has pulled some dirty cheap maths trick to completely skip out the solution of the differential equation. His solution doesn't look right to me. If you are deriving SHM you need to find the solution of the 2nd order differential equation of motion in terms of time and then plug in arbitrary boundary conditions for t to find the period of oscillation.

The page linked below is good, and serves as a decent reminder. The trick is remembering that the solution of the 2nd order ODE is of the form

X = A.cos (w.t - phi)

Where the phase shift (phi) in the web example is just assumed to be zero. You can then just differentiate the above twice and plug directly into

X'' = -(k/m).t

The solution X = A.cos (w.t) makes sense if you think about it. A is the amplitude of the oscillation, and if undamped, the mass will follow a sinusoidal (or cosinusoidal, effectively the same thing) pattern of motion.

Also, this forms part of the fundamental basis of all engineering disciplines, so no need to change the title.

http://m.sparknotes.com/physics/oscillations/oscillationsandsimpleharmonicmotion/section2.rhtml

My advice - learn it the proper way and ignore the lecturer's cheap maths tricks. I'm not even convinced they are right. Best not to rely on that stuff.

X'' ~ x ?????

No idea where he has pulled that from or how it even helps with his algebra. Looks like nonsense.
 
Last edited:
Thanks guys, I will have a look at the links you've provided.

Hopefully I'll be able to get back on track and it'll begin to make a bit more sense now!
 
You must log in or register to reply here.
Back
Top Bottom