Tricky mechanics problem! The Tarzan problem

engstrom0304 · 28 May 2012 at 17:46

Hey guys...

This is a tricky mechanics problem that I'm trying to solve and then do an experiment to prove for my a2 physics coursework.

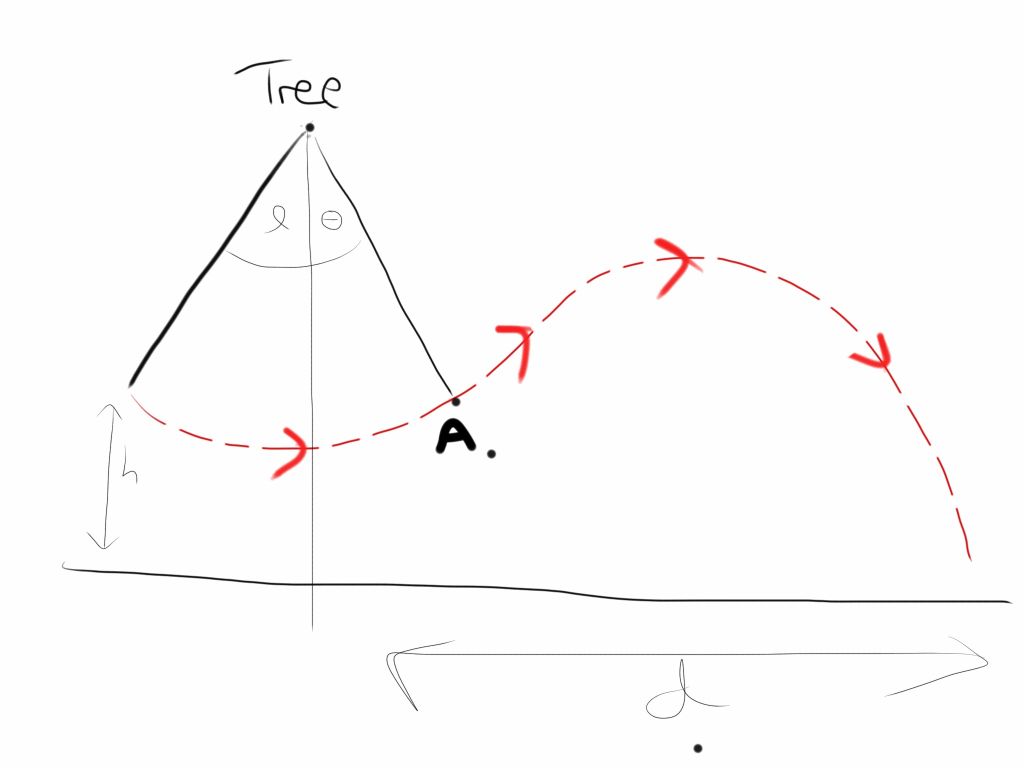
It could be called the Tarzan problem...

Tarzan is swinging on a vine... He lets go at a certain point and falls to the ground as a projectile... The question is, given the initial height of the start of the swing from the ground, that the initial velocity is 0 and the length of the rope, when should Tarzan let go of the vine?

I think that to find the speed at any height above the ground for the vine part it is easiest to use conservation of energy laws? What do you guys think to this problem?

A. Is the point where Tarzan lets go of the vine

Edit:
d is from the centre point.
Aim is to achieve maximum distance
I'm pretty sure finding the speed at any point on the vine is best via conservation of energy, assuming air resistance is negligible
Alpha, h and the mass of Tarzan are constants, the mass is m kg

RomanNose · 28 May 2012 at 17:48

45 degrees I think is the rule of projectiles to maximize distance. But I am struggling to explain why.
What you need to do is find the horizontal distance in terms of theta and vertical velocity then try to maximize it.

estebanrey · 28 May 2012 at 17:48

engstrom0304 said:
when should Tarzan let go of the vine?

Surely that depends on what Tarzan is tryting to achieve which seems missing from your OP. Are we to assume he's trying to get the longest distance forward (D)?

mistercrabb · 28 May 2012 at 18:02

RomanNose said:
45 degrees I think is the rule of projectiles to maximize distance. But I am struggling to explain why.
What you need to do is find the horizontal distance in terms of theta and vertical velocity then try to maximize it.

I say 45 degrees too. Isn't it because at that point you have the highest combined horizontal and vertical velocity?

But there isn't enough data to know what the question is actually asking.
OP can you post the actual question?

mollymoo · 28 May 2012 at 18:13

RomanNose said:
45 degrees I think is the rule of projectiles to maximize distance. But I am struggling to explain why.
What you need to do is find the horizontal distance in terms of theta and vertical velocity then try to maximize it.

Because of track and field on the spectrum I think.

The__Malteser · 28 May 2012 at 18:15

It is indeed 45 deg. Don't ask me why, but I'm sure of it. Studied it a few years ago!

Jjustme · 28 May 2012 at 18:19

I don't think we can give an exact answer such as 45.
We don't know what alpha is, if it was 1 deg, he won't even make it to 45 deg.

But I'm guessing it's where theta = alpha/2 because that'll be where he has 1/2 max velocity and 1/2 max angle.

touch · 28 May 2012 at 18:22

My guess would be alpha/2

edit: beaten

Philip Perfect · 28 May 2012 at 18:22

The__Malteser said:
It is indeed 45 deg. Don't ask me why, but I'm sure of it. Studied it a few years ago!

Not necessarily, I don't think. As Tarzan swings upwards on the rope, he'll be slowing down - 45 degrees would assume the launch speed is the same everywhere. You'll need to find a formula for the distance travelled as a function of launch angle and speed, find the speed as a function of the launch angle (using the pendulum part), and that should give you the answer.

Good luck!

GreatAuk · 28 May 2012 at 18:35

I'd start by getting all the terms you're interested in into an equation, and then I'd do some calculus. As I have nothing better to do, I'm going to give it a go

Edit: is 'd' measured from A, or from directly below the pivot?

estebanrey · 28 May 2012 at 18:37

Philip Perfect said:
Not necessarily, I don't think. As Tarzan swings upwards on the rope, he'll be slowing down - 45 degrees would assume the launch speed is the same everywhere. You'll need to find a formula for the distance travelled as a function of launch angle and speed, find the speed as a function of the launch angle (using the pendulum part), and that should give you the answer.

If you're going to consider the above you'd also need to know the weight of Tarzan and the area of a front profile to calculate wind resistance.

RomanNose · 28 May 2012 at 18:40

If you want marks then just do the simplest coursework possible.
Both my Electronics and Physics courseworks were quite complex, the marks were fine but I know people who put half the work in and got the same mark.

GreatAuk · 28 May 2012 at 18:52

estebanrey said:
If you're going to consider the above you'd also need to know the weight of Tarzan and the area of a front profile to calculate wind resistance.

I think Philip's just talking about slowing down due to action of mavity rather than air resistance.

dirtychinchilla · 28 May 2012 at 19:01

If his velocity at A is zero then he will fall to the ground...

Jjustme · 28 May 2012 at 19:03

dirtychinchilla said:
If his velocity at A is zero then he will fall to the ground...

That would be true if both angles were the same.

estebanrey · 28 May 2012 at 19:03

GreatAuk said:
I think Philip's just talking about slowing down due to action of mavity rather than air resistance.

But why consider one factor and ignore another?

Besides you'd still need to know Tarzan's weight to calculate the maximum speed he will achieve.

D D Danneh · 28 May 2012 at 19:14

estebanrey said:
But why consider one factor and ignore another?

Besides you'd still need to know Tarzan's weight to calculate the maximum speed he will achieve.

I don't know how to use air resistance in anything other than a linear problem

Also, you don't need to know his weight at all, mass is pretty much immediately cancelled out once you start using energy methods.

I get, for D:

edit: correction, the first part of that should be rsin(theta)(1+2cos^2(theta)-2cos(theta)cos(alpha))

D being the distance from the centre of the arc to the point tarzan lands at, r being the length of the rope (pretty sure this is required), and h being the height from the ground to the starting point of the swing.

No idea if that is right, but I think the methods I've used are fine, any errors will be typographical

Jjustme · 28 May 2012 at 19:25

D D Danneh said:
I don't know how to use air resistance in anything other than a linear problem

Also, you don't need to know his weight at all, mass is pretty much immediately cancelled out once you start using energy methods.

I get, for D:

edit: correction, the first part of that should be rsin(theta)(1+2cos^2(theta)-2cos(theta)cos(alpha))

D being the distance from the centre of the arc to the point tarzan lands at, r being the length of the rope (pretty sure this is required), and h being the height from the ground to the starting point of the swing.

No idea if that is right, but I think the methods I've used are fine, any errors will be typographical

Yikes, that looks complicated, I hope you read that the question asked when he should let go, not how far he would travel and just wanted to work out d as a mental exercise.

Reaper 392 · 28 May 2012 at 19:31

not remembering the equations you need for a pendulum in motion really isnt helping me. however, this is how i would tackle the question (it may not be the best way since i havent done mechanics for several years)

first i would derive one equation for tarzan's velocity going upwards and another equation for tarzan's velocity going sideways at any given angle of release.

you will then need to plug the vertical speed into a suvat equation to work out how long tarzan will stay in the air (this answer will still have a lot of variables). this is where you would plug in your H, taking into account that tarzan is swinging along the arc of a circle, so he will not release at a height of H

next you use your 'horizontal speed' of tarzan and your 'time in the air' values into yet another suvat equation to determine his distance travelled.

to find the maximum distance travelled you will need to use differentiation. i'm ashamed to say that i cant remember exactly how to do this, but i know it involves differentiating twice

its seems like a very complicated way of doing things, but i cant see any other way of doing it with my very limited amount of knowledge

D D Danneh · 28 May 2012 at 19:32

Jjustme said:
Yikes, that looks complicated, I hope you read that the question asked when he should let go, not how far he would travel and just wanted to work out d as a mental exercise.

To be honest, asking when to let go makes it a little harder because then you have to look to maximise D. I'm not sure if what I've got works though, because that would mean if both alpha and theta are the same, then the height is irrelevant, as h only factors in with h(cos(theta)-cos(alpha)), which would be zero if theta = alpha :/ Obviously height does matter, because that increases the time it takes to reach the ground.

Reaper 392 said:
not remembering the equations you need for a pendulum in motion really isnt helping me. however, this is how i would tackle the question (it may not be the best way since i havent done mechanics for several years)

first i would derive one equation for tarzan's velocity going upwards and another equation for tarzan's velocity going sideways at any given angle of release.

you will then need to plug the vertical speed into a suvat equation to work out how long tarzan will stay in the air (this answer will still have a lot of variables). this is where you would plug in your H, taking into account that tarzan is swinging along the arc of a circle, so he will not release at a height of H

next you use your 'horizontal speed' of tarzan and your 'time in the air' values into yet another suvat equation to determine his distance travelled.

to find the maximum distance travelled you will need to use differentiation. i'm ashamed to say that i cant remember exactly how to do this, but i know it involves differentiating twice

its seems like a very complicated way of doing things, but i cant see any other way of doing it with my very limited amount of knowledge

That's precisely what I did, and I'm about to double check it