You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Wonderfully logical illogical probability problem
- Thread starter OSB
- Start date
More options
Thread starter's postsCaporegime
- Joined
- 20 Oct 2002
- Posts
- 78,182
- Location
- Wish i was in a Ramen Shop Counter
There are four configurations of children:
Youngest first the possibilities are GG, GB, BG, BB (G - Girl, B - Boy) and all are equally likely.
First situation.
BB of them is ruled out by knowing that one is a girl.
Thus, we only have GG, GB and BG left.
Knowing that the child with him is a girl gives a 1/3 chance that he has another girl and 2/3 chance that the other child is a boy.
Second situation.
We now know that the youngest child is a girl, this leaves only GG and GB.
Thus the probability is 1/2 that the other child is a boy.
Hope that's right!
But surely, regardless what he says, the sex of each child is independant of the next one, so it is ALWAYS 50% the other child is a boy.
But surely, regardless what he says, the sex of each child is independant of the next one, so it is ALWAYS 50% the other child is a boy.
But you're given some information (i.e. that one of the children is a girl) so this narrows down the options.
At this point you know that it's impossible for him to have 2 boys.
Think of it this way, you have 2 yellow balls and 2 red balls.
2 of these are put into a box, but you don't know which ones.
You pull out the first ball and it's yellow.
What is the probability of the second ball being red?
This is exactly the same problem, the answer is 2/3.
There are twice as many ways to arrange a yellow ball and a red ball (YR and RY) that there are to arrange two yellows (YY) thus the situation of this occurring happens twice as often as getting another yellow (so probability of this is 1/3)
Caporegime
- Joined
- 18 Oct 2002
- Posts
- 37,798
- Location
- block 16, cell 12
I had to work this one out this morning, i first thought wtf!? Then i worked it out, see what you think:
You meet your new tutor in town accompanied by a young girl. He says to you "I have two children, this is my daughter Lisa". What is the probability that his other child is a boy. Would it make a difference if he had said "I have two children, this is my youngest child, Lisa"? (You may assume a 50% chance of any one birth being a boy or a girl.
Have fun!
OSB
no, if the 2nd part had this is my youngest "daughter" then it would alter the chance, otherwise not.
also, surely each child is an independant event and yes each birth will yield a 50/50 (if that is the % of boys to girls born?), regardless of the child before, the womb does not keep count.
chance of having a child being a boy or a girl= 1/2
generally, if you're having 2 children:
a)chance of having two boys = 1/2 x 1/2 = 1/4
b)chance of having a boy then a girl = 1/2 x 1/2= 1/4
c)chance of having a girl then a boy = 1/2 x 1/2= 1/4
d)chance of having two girls = 1/2 x 1/2 = 1/4
second child = a girl therefore the probability, in this case, of your second child being a girl is 1
a)boy then girl = 1/2 x 1 = 1/2
b)girl then girl = 1/2 x 1 = 1/2
as you can see, each situation has the same chance. so it's a 50% chance.
generally, if you're having 2 children:
a)chance of having two boys = 1/2 x 1/2 = 1/4
b)chance of having a boy then a girl = 1/2 x 1/2= 1/4
c)chance of having a girl then a boy = 1/2 x 1/2= 1/4
d)chance of having two girls = 1/2 x 1/2 = 1/4
second child = a girl therefore the probability, in this case, of your second child being a girl is 1
a)boy then girl = 1/2 x 1 = 1/2
b)girl then girl = 1/2 x 1 = 1/2
as you can see, each situation has the same chance. so it's a 50% chance.
Soldato
- Joined
- 5 Mar 2006
- Posts
- 6,183
- Location
- everywhere
.
Last edited:
I'm sorry to say this is absolute tripe!
have you ever heard of a tree diagram?
because that is just a tree diagram without the pretty pictures.
Soldato
- Joined
- 5 Mar 2006
- Posts
- 6,183
- Location
- everywhere
.
Last edited:
If you don't know the gender of either of the children, the tree looks like this:
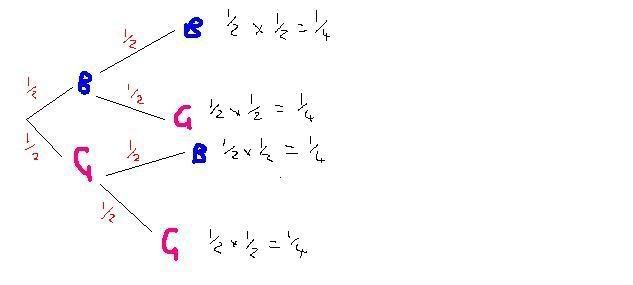
if you know that one of the children was a girl, (let's say that the girl was the oldest child (it doesn't matter which way around it is for the maths)) the tree diagram looks like this:
As you can see, there's a 50% chance of girl+ boy, and there's a 50% chance of girl+ girl.
Thanks.
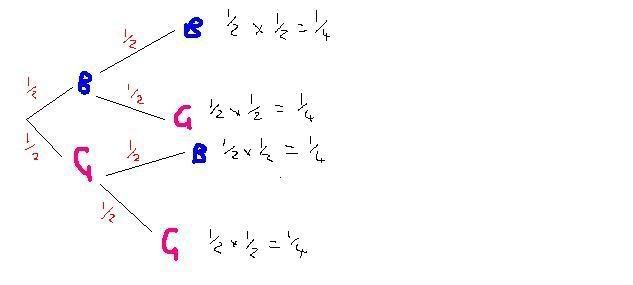
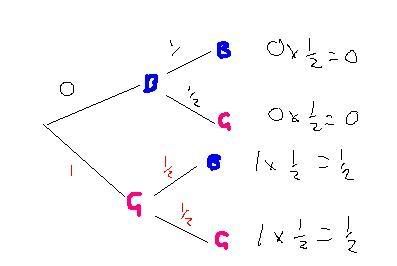
if you know that one of the children was a girl, (let's say that the girl was the oldest child (it doesn't matter which way around it is for the maths)) the tree diagram looks like this:

As you can see, there's a 50% chance of girl+ boy, and there's a 50% chance of girl+ girl.
Thanks.
This is nothing to do with the womb keeping count.no, if the 2nd part had this is my youngest "daughter" then it would alter the chance, otherwise not.
also, surely each child is an independant event and yes each birth will yield a 50/50 (if that is the % of boys to girls born?), regardless of the child before, the womb does not keep count.
Let's take it to extremes.
Imagine the tutor has 10 children, you meet him with 9 of his children and those 9 are all girls.
What is the chance of the other child being a boy?
In this case it is 10/11
The probability of having 9 girls and 1 boy is 10 times as great as having 10 boys.
This is because you can have GGGGGGGGGB, GGGGGGGGBG, ..., BGGGGGGGGG
Given that you know 9 are girls you have eliminated any other possibilites, e.g. 7 boys and 3 girls.
The point of this is that by knowing the fact that the child (or 9 of them) is a girl eliminates some of the possibilies.
EDIT: Ben M, the second branch down (B then G) isn't 0 as you can't make the assumption that the girl is the oldest.
If you don't know the gender of either of the children, the tree looks like this:
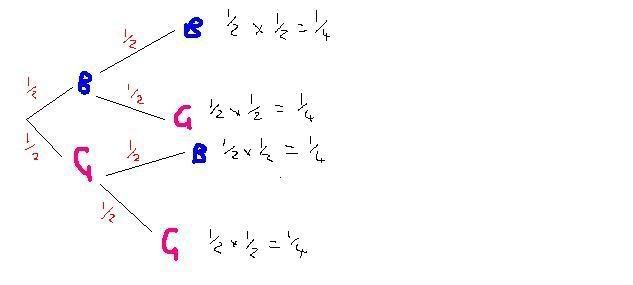
if you know that one of the children was a girl, (let's say that the girl was the oldest child (it doesn't matter which way around it is for the maths)) the tree diagram looks like this:

As you can see, there's a 50% chance of girl+ boy, and there's a 50% chance of girl+ girl.
Thanks.
But in the first case you still canoot have BB therefore your diagram is flawed, trust markyp23 he has the correct answer as counter intuitive as it seems!
That statement is wrong, for the reason that GB = BGThere are four configurations of children:
Youngest first the possibilities are GG, GB, BG, BB (G - Girl, B - Boy) and all are equally likely.
The fact is having a daughter does not alter the chance of having a boy/girl from 50/50 as the other child as they are independent.
Edit: Actually my first statement is wrong I was thinking of the non ordered case, but the second is right, give that the youngest is stated as female makes BG and BB impossible, only GG and GB are valid, reducing to G or B as we know the first G is 100% probable.
That statement is wrong, for the reason that GB = BG
The fact is having a daughter does not alter the chance of having a boy/girl from 50/50 as the other child as they are independent.
No it's not.
The boy could be older or the girl could be older.
If there are two children P(Boy first then Girl) = P(Girl first then Boy) = 0.25
I'm always amazed how many people don't get it when things like this are posted.
Just seen your edit, you've seen the light

Edited it in why it's wrong.No it's not.
The boy could be older or the girl could be older.
If there are two children P(Boy first then Girl) = P(Girl first then Boy) = 0.25
I'm always amazed how many people don't get it when things like this are posted.
By stating that the daughter is younger reduces the options to either the other child being female or male, there's no chance of their being two sons. It's 50/50 as a result.
Edit: Ben M's diagram shows why.
Soldato
- Joined
- 5 Mar 2006
- Posts
- 6,183
- Location
- everywhere
.
Last edited:



