I had to work this one out this morning, i first thought wtf!? Then i worked it out, see what you think:
You meet your new tutor in town accompanied by a young girl. He says to you "I have two children, this is my daughter Lisa". What is the probability that his other child is a boy. Would it make a difference if he had said "I have two children, this is my youngest child, Lisa"? (You may assume a 50% chance of any one birth being a boy or a girl.
Have fun!
OSB
You meet your new tutor in town accompanied by a young girl. He says to you "I have two children, this is my daughter Lisa". What is the probability that his other child is a boy. Would it make a difference if he had said "I have two children, this is my youngest child, Lisa"? (You may assume a 50% chance of any one birth being a boy or a girl.
Have fun!
OSB




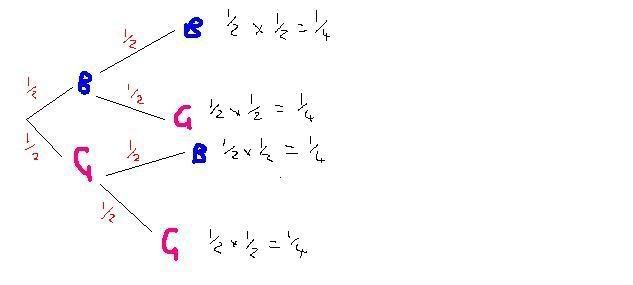
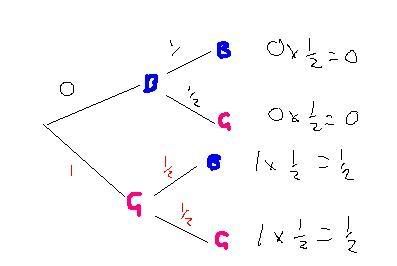
 .
.

